the Poincare conjecture
I suggest that the Poincare conjecture is a direct result of a new understanding of the basic structure of space itself.
In the concept sharing of a point, we can see that space has this new leveled structure.
Abstract: Here I introduce concept sharing. In uncovering extended space, I develop new ways of understanding Poincare’s conjecture.
Mathematical Concept removal and sharing
Introduction:
The notion of a point, that which has no parts or no extent, is basic in math. The ancient Greeks thought about points, but what if they were not entirely correct?
They asked, what if two points were placed next to each other? They thought that this would be one point and stopped there.-Aristotle : Physics- “neither can two points be contiguous with one another”
But what if this could be regarded as two points? Since something of no extent placed next to something of no extent would have no extent- but there could be two items of no extent there! The two points could be hidden as one!
Yet, as Aristotle thought the two indivisables of no parts would overlap for the two items can be considered together, side by side or to be on top of one another. This is possible with items of no extent as we can consider them either to be on top of each other or side by side. If two dots are placed side by side, they can be considered on top of one another if we look at them from the side. Also if two dots are placed on top of one another we can look at them as being side by side from the top.
Since we want to keep this concept of no extent, or no parts it must also be possible to have two together and still have two, as long as the two parts are different entities so that they do not combine into one. That is, there must be another possible entity with no extent!
One can regard the overlapping shadow diagram below:
Consider a teacup placed on a table with two lights from above. One from the left and one from the right. See below:
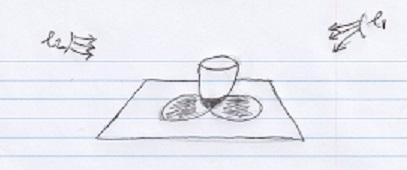
Now as seen in the overlap, two different points of the shadows can take up the space of one point, we can regard these as e( e is another possible entity of no extent) and p and not points, p and p. If I take away one light, one shadow still remains.
This concept cannot be visualized as one would be trying to visualize two different items in the same place, but it is still logical, nonetheless. Even the concept of no extent cannot be fully visualized as well. Only usually we represent a point with a dot, but this is not really a visual of an object with no extent.
Also, consider that we have to take a point out in order to have this e*p present. That is e, the new entity sharing position with the point, p. That means we need another level to place, this must exist since we have to have e*p somehow.
Then this is how e can be made different from p, as in an extent of e and p which can come about, we can move e through this e extent, it then has a new location of original location, making it different from p. That is, e is the next level of location.
Yet we want this concept of point removal and sharing (the point is removed and the two points are sharing the notion or concept of an object of no extent) to join up with the knowledge that is already in existence.
In doing this we have to add to and change the mathematics which already exists. This turns out not to destroy but heal mathematics, as this can be seen as something which is basic, but is missing. The math from this leads to a way to solve many old problems which are easy to state but previously hard to solve, such as:
The knot problem:https://calctutor.ca/category/mathematics/knots-mathematics/the-knottedness-and-chirality-of-the-trefoil/
The twin prime conjecture:https://calctutor.ca/category/mathematics/the-twin-prime-conjecture/
The Goldbach conjecture:https://calctutor.ca/category/mathematics/goldbachs-conjecture/
Fermat’s last theorem;https://calctutor.ca/category/mathematics/a-clearer-and-simpler-demonstration-of-fermats-last-theorem-wiles-theorem/
The Poincare conjecture:https://calctutor.ca/category/mathematics/the-poincare-conjecture/
The Riemann Hypothesis:https://calctutor.ca/category/mathematics/the-riemann-hypothesis/
The Collatz conjecture:https://calctutor.ca/category/mathematics/the-collatz-conjecture/
In fact this idea can complete mathematics:
The completion of mathematics:https://calctutor.ca/category/mathematics/the-completion-of-mathematics/
Definition and description of e:
When two points come together or start together, it seems as if there could be two there as 0+0=0.(two items of no extent could still combine to no extent). Only that points have location only, and having them together means we have one location so we have to conclude that there is one point there.
What if an object of no extent could be expressed as two different items of no extent, starting together. Since an item of no extent together with another different item of no extent would still have no extent, yet there could still be two items here and not one. The other item of no extent would have to have something more than location (it would have to be different from a point).
Yet since it is logical that two items of no extent could be together and still be two items, this must be mathematically possible, somehow. It would work if the two items were not both points, in the sense that they were not the same type of entity. For points are defined to have location only and here we are at the same location.
Call this new indivisible item “e”. Then this together with a point can be called e*p. We can separate e and p (not divide as this is a separation not a division) if we move the original e along an extent made up of e’s. This extent of e’s can be together with an extent of p’s. The e extent is different from the p extent in that it is a series of positions of the original e position. That is it is the next level of position.
Then we have to have an object of no extent which is somehow different from the usual conception. I am thinking of putting two items of zero size together. One can think of putting a dot on top or beside a dot which is there already. One cannot visualize two items of no extent being together, but one can also not visualize an item of no extent as well.
Yet they are an e( new entity) and a point (p) at the same place, if we have a preexisting space made up of ordinary points (p’s).
In terms of symbols, one may write pop=p as the idea that for an ordinary point two points starting together or being brought in coincidence form again an ordinary point. O is the idea of coincidence.
Then e would be something different. E then cannot be in coincidence with p, if we redefine coincidence as the starting together or coming together of two or more points. so we invent a way for the entities to be together and call it sharing, E*p is e sharing with p . Sharing is a way for two items to come together or be defined together and not combine. This should be possible as seen in the analogy of the overlapping shadows. This must exist somehow in mathematics, since we must have the notion of something with no parts or no extent and we can put two together and still have two. So we have p and e as different entities which are not identical.
Additionally we must remove p for p*e( p and e together) to exist otherwise there is confusion. If we start with a space with P’s everywhere we have to remove a p to put in an e*p. So there must be another level to space. A container of points and e’s. This would then be a new place of original places, another level to place. Then we can see that e can be different from p, as in an extended space of e’s, I could move an e to another new place of the original place of e, along the e continuum. The e continuum can coexist with the p continuum.
So e is another type of point. It is able to be with another entity which has no extent and not be equal to that entity. P doesn’t share with p, as this is already seen as coincidence. Since points have location only this is the same location and so the same point.
Looking at e, e(1)oe(1)=e(1). But also possible is e(1)(e(2)), if we have an extent of e outwards from p(1). e(2) is some e on the e extent outwards from p(1). This is what makes e different from p, with p we only have pop=p. That is an e can act as a type of container for other e’s, as two different e’s do not combine similar to a p and an e. That means we can have a shifting movement of one e along another continuum of e’s. Then e’s can have a new location of the original location of an e which makes them different from p’s, which have location only.
e(1)*p(1) is e and p sharing a location. We can separate a copy of e(1) away, since 0-0=0. Think of a jigsaw puzzle of a landscape being taken apart. e(1)*p(1) =e(1)oe(1)*p(1). Let e(0) be a bridge into the other dimension. Then e(0)(e(1))oe(1)*p(1)=(e(0)*e(1))o*p(1) and p(1) falls away leaving e(0)(e(1)). Then we have e(2)(e(1)) with e(1) moving to an e(2). There might also be an extent of p, along with the e, In which case we can have e(1)*e(2)*p(2).
The e can be multiple, also e can move along another extent of e’s. This is how e is different from p.
To be complete…=p(1)op(1)op(1)op(1) =p(1)op(1)op(1)=p(1)op(1)=p(1), and also….=e(1)oe(1)oe(1)oe(1)=e(1)oe(1)oe(1)=e(1)oe(1)=e(1) and also.. e(1)*e(2)*e(3)*e(4) is not equal to e(1)*e(2)*e(3) is not equal to e(1)*e(2) is not equal to a single e .Also e(0)(e(1)*e(2)*…)). That is, e or multiple e’s can travel along an extent of e’s.
These would not be points, then, as points have location only. Two moving points could come together to form one point. In Physics or mathematics if we have a plane of points(fixed) there can be a point moving in this plane which takes up the locations of these planar points as it moves, and then we have pop=p as it moves.
But also e’s can move as well and we could have two e’s come together to form e*e when the initial location is moved to the extent of e’s.
A point is the notion of that which has no extent or location only, labelled, p.
But since the idea of no extent is to have no dimension.
Two ‘items’ of no extent could exist together and still have no extent. The sum of any number of these new items of no extent is also no extent. The two will be hidden as one. They are hidden as one, at the ordinary point in the pre-existing space.
It would be two of these new locations at a regular location. By regular location, we mean an ordinary point of the pre-existing space.
Since points have location only, and not this multiplicity, this could not be two points, but would have to be two of something else, call them ‘parts’.
Represent them by the letter e.
e has no extent but can also be multiple. E’s have the position to them given by the pre-existing points of the pre-existing space.
Two little nothings still add up to nothing, yet there can be two little nothings there. The two items would just be hidden as one. Let’s hide!-they say. Who can see us? The two items would not be points, for points have a singularity to them. That is, when I combine two moving points, in the usual geometry, it leads to one point, but this doesn’t have to be so with another possible entity.
These two items could be multiple. This is how we can hide! In order to do this we would have to take out the usual concept of a point as being the only entity with no extent and replace it with these new conceptions as other entities which can have no extent. There are these little entities that don’t combine to form a point. This is because a point is already there as the only idea of no extent. We need some room!
If you accept the notion of an entity with no extent you have to accept this new possibility as well. If you want a point, you have to have us too! The new entities say! The notion of no extent leads naturally to concept sharing! The concept of no extent is an example of a concept.
To remove the concept of a point as the only item of no extent, we need to have a concept space, consisting of a concept of multiplicity. This must exist because I must have this further concept of a doubled item of no extent somewhere and I need to take out the concept of a single item as the only item of no extent to have it appear somewhere. Also we must take out any other possibility of any number of items, except 2.
Extension to other concepts:
Furthermore, all math concepts are point-like in that they are exact ideas which have no existence in physical reality. They are mental constructions which are not available to the senses. They are in thought only.
We can replace e and p, as two items sharing the concept of no extent with two items sharing the concept of a number as well. Or the concept of a set, or group, etc.
Math concepts are exact so that they don’t change from person to person or over time or space. A number, point, function or group, etc. is unchanging, eternal, unalterable.
So also they all can be multiple as the basic ideas of math are all based on geometry and numbers. Functions map inputs to outputs based on formulas which are algebraic expressions of variables(numbers) to points on a graph. Groups are collections of the rotations or flips of geometric objects. Elements of groups are exact in the end numerical or geometric. So numbers, sets, groups, functions, etc. can all have concept spaces!
The idea is to extend the concept using the idea of the concept and the extender “of”. So for example; location of location, number of numbers.
The idea is to go backwards into the idea.
Look at the example of location. For a new location of an initial location we need an extended location, that is there must be an extended location, somewhere to put one of the entities, the extended entity.
Then the extended entity has the location of an initial location, which makes it different from a point, having only location.
The concept sharing of a number:
We can start with a line of p’s with two lines of e’s sharing locations. All in a plane of e’s as shown below:
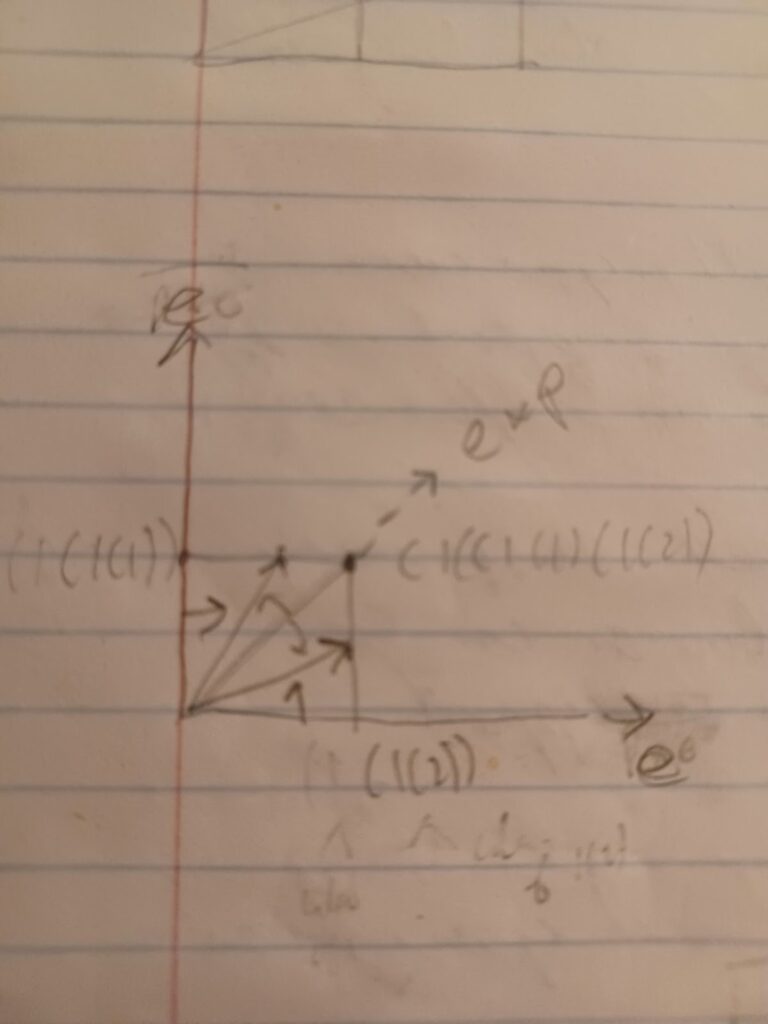
The numbers 1, 1(1) and 1(2) can be associated as shown, an e is removed and replaced with an e*e and we can associate the new numbers 1(1) and 1(2), concept sharing with the number 1. The number of numbers is 2 and not 1. We can then unfold the two lines of e’s to make an axis where we can have the numbers 1(1) and 1(2). The two numbers 1(1) and 1(2) are sharing the concept of 1, with 1 on the number line. We have the usual number line on the midline of the new plane.
With numbers, they represent a position, an amount or a label.
Think about position and consider a race where 2 runners are tied for 10th place. We can say the runners are tied for tenth place giving the number 10 to both runners. But suppose instead of a foot race, two points are together in a race along the number line. Then in 10th place two points could be together as has been seen. Then two number 10’s can be given one to each point. These numbers could go with the points as they are mapped into the new plane which has been mentioned.
A circle which is the 10th circle to be formed could contain the two e’s with the two number 10’s. Then 10(1) and 10(2) could also show an amount of points, 2. As well these could be the labels we are giving to these points, or the position in a number line, 10.
If sets are made of points, the sets could have concept spaces. If sets were made of numbers, the numbers could be associated with points and we could have concept spaces. Similarly if groups are made of numbers or diagrams which are made of points they too could have lower concept spaces.
In the equation x^2+y^2=1 the two points (0,1) and (0,-1) can be mapped to the point (0,0).
This can be notated ….p(1)*p(2)*p(3)=p(1)*p(2)= p(0).
Where * is the idea of different points coming together in the usual plane.
When mapping to points there is a many to many map, a many to one map or a one to one map. Yet there is another possibility with e’s. There can be, for example, a two to two map. Where two separated e’s are in the new plane and combine to form two e’s at a single location. I say two e’s at that location now because they are defined in two different places in the new plane. Therefore there are two here as in the case of the overlapping shadows.
Since it is possible to have two entities together and still be two entities, this other case must exist somewhere. The entities must be zero-dimensional but not be points.
Yet the overlapping shadows show us that there could be a constant number of entities. This is because the shadows have somewhere to be cast onto. Rather than a notion of no extent alone, which could or could not be multiple, the surface makes it possible to show a finite number of entities of no extent.
Then postulate a place of places where ‘e” the entity of no extent which is like a point in that it has no extent but unlike a point being different in the following way:
e(0) is not equal to e(1)*e(2) is not equal to e(1)*e(2)*e(3) where again * is the idea of movement but this time in the new plane.
Suppose I represent a location by (0,0). What if we can have a case of (0,0)(1) not equal to (0,0)(2)?. This is possible if (0,0)(1) and (0,0)(2) were somehow different. Since something with no extent can be “added” to something with no extent and the result is something with no extent, there could be two items here. (see the overlapping shadow diagram) We would have to somehow make the two “points” different and only two “points”.
Since two items (“points”) of no extent could appear to be a single item, and we could conceivably fix this at 2 or three, or as many as we choose, this other plane also must exist.
The usual idea of points can be notated …p(1)*p(2)*p(3)=p(1)*p(2)=p(0).This is the idea of two or more points coming together to form one point. This is all happening in the usual plane.
The other case can be notated e(0)=e(0) not equal to e(1)*e(2)=e(1)*e(2) not equal to e(1)*e(2)*e(3)=e(1)*e(2)*e(3). So e is not equal to p because it exists in placement space and has this other feature which is different from the way p behaves. In placement space we have 1 or 2 or 3 e’s together and also capable of being separated to different placements.
Then usually the idea of points can be notated pxp=p or pxpxp=p…etc. Where x is the idea of coming together or separating apart and p is a point. But what if there were another entity of no extent, call it e such that exe=exe, e is not equal to p so that exe is not equal to p and also exe=is not equal to e as that would be the same as pxp=p. We can call these entity equations.
It seems like exe are two identical entities of no extent and it should result in e. But consider that to have exe=p, I have to take out pxp=p that is the idea that a point is the only item of no extent.
This means I need a space of places coexisting with the original places, so that I can take out the place pxp=p and replace it with the new places, exe=exe. Then we give up the notion of a fixed plane of points, instead we can have three planes, coexisting with one another.
The most basic new plane is in a sense at a lower level than the usual plane. This is a plane of places of new places .Any e in the usual plane can move off in any direction into this new plane, leaving its partner behind. Most basically, the entire plane can move, as shown above.
That means exe are not 2e’s at the same place, as is usually thought of as place but two e’s at the same place in new places. A new level to place. Now we have more room. Since they are in this sense not in the same place, they don’t combine. Briefly we can write this exe=exe (sharing).
Take out the concept of place and put in this new concept of place. The only way it can be different is if the places don’t combine to form a single place but stay separate while being together. (sharing as in the overlapping teacup shadows)
Then we can separate the two e’s, but the only way this can be different from the usual idea of separation in points, They are the same in that they share a place and a place of new and original places.
The place has been removed so we have an underlying dimension where places have other places of original places. Like a jigsaw puzzle of a landscape being taken apart. In this way two e’s are sharing a place and a place of new places.

Then this leads to a new extent, a line with two distances one being this new zero and the other being the usual concept of distance, extended.
Wait, the little entities say, how can this help anything mathematical? We can just scatter anywhere! Yes but you could also stay together as a line!
Then this leads to a new extent, a line with two distances one being this new zero and the other being the usual concept of distance, extended.
This is a new dimension. Each e of the extent is different as any other e, yet they originally shared. This is just a new dimension in length. We can notate any two e’s as e(1,m) and e(1,n).
This extent may be considered as negative distance as we need to shrink it to get back to the new zero and then take this out and replace it with pxp=p to get back to the usual zero. Since for e(1,m) and e(1,n) the place is the same, any point that is bound to e(1,m) is also bound to e(1,n). Just not to both at the same time. We may have a closed loop of e’s which can move off and the shape could be altered if we have different distances associated with each e.
We can set a mathematical system with exe=p or choose three e’s so that exexe=p or the number of e’s could be variable.
This must fit into our current structure of mathematics as I am not adding any new notion in, merely clarifying the concept of a point as having no extent, then adding in the necessary new entities. The notion of no extent is the same. We already have this notion of a point as being pxp=p, we have to extend this.
Additionally, there is also the case exr=exr where e and r are two different types of entities as well. This can be for future work.
So we have the idea that a point is an entity with no extent, and also another notion that it could be exe=p but how do these fit together?
It must be that we have replaced the usual idea of a point as being pxp=p with this new idea of a point as being exe=exe.. This is the space, the space of doubled e’s. It can be modeled after the usual idea of extent, yet the distances are negative.
Then this also means I can separate exe=exe in the new space and move in a space between two of the same e, like so, the displacements from the 2e’s are shown.
Then we can have the idea of a multiple point or two tangent points.
With the tangent point we measure the diameters from the point of tangency outward. These can be separated as usual with the usual distance appearing between them. The exe=exe points can be separated as well, with the new space appearing between them.This is the space of places of new places. This is the negative space.
So we must have a plane or a space in which the ordinary places e or p, take on other places.
A picture of this would look like below if we have only two e’s at the origin and I move one e off up and to the right.: The notation is (()) are places of new places and () are places.
This is a movement of one piece of a doubled origin, a single e.
Not only the origin but each identified exe=p of the new space can act as its own centre, The two e’s can move away from each other.
We could have a closed loop of these points all moving together as shown in the diagram above. As well, this loop could be knotted, if instead of a plane we consider a three dimensional space..
Then this is also the entry into Concept Sharing as math concepts such as number, set, group, ect. Can all be thought of as point-like. That is to say they are all ideas which could have multiple expressions. They can all have sharings.
They are all exact and have no physical reality, they are just ideas.
Since they can all be multiple, there must exist lower concept spaces.
The Concept Sharing of a number:
A number is an amount, as in a counting number, or a position on a number line, or a label.
It is point-like in that it has no existence in physical reality, it is a mathematical object, not a physical object. Therefore we can make a correspondence between the idea of sharing in points and an idea of sharing in numbers.
So that means the concept of a number can be extended downwards so that we have a number of original numbers space and this number of sharing numbers after we take out the original number. So, for example, with the number 1; we have a number of numbers space, let the number of original numbers be 2, instead of 1. Take out the number 1, then we can have 1(1) and 1(2) sharing.
So also that any loop may be considered to be a point, because the point can have an infinite number of parts, and any point considered to be a loop. Therefore any space which does not contain “holes” or twists in any dimension will be necessarily simply connected.
